
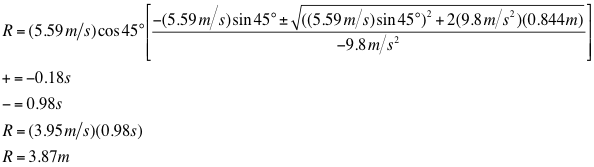
But we're going to assume that it does, that this does not change, that it is negligible. Would not stay constant while it's traveling through the air. Significant air resistance, this horizontal velocity And, once again, the assumption that were making this videos is that air resistance is negligible. How long it's in the air, we can multiply it by, we can multiply it by the horizontal component of the velocity, and that will tell us how far it travels. Its vertical component is gonna determine how quickly it decelerates due to gravity and then re-accelerated, and essentially how long it's going to be the air. Because it doesn't matter what its horizontal component is. In the upwards direction, and we can figure, we can use that to figure out how long will this rock stay in the air. Vertical component, some amount of velocity So this velocity vector can be broken down into its vertical and its horizontal components. We're going to use a vertical component, so let me just draw it visually. This velocity vector into its vertical and And what we want toįigure out in this video is how far does the rock travel? We want to figure out how, how far does it travel? Does it travel? And to simplify this problem, what we're gonna do is we're gonna break down Or the angle between theĭirection of the launch and horizontal is 30 degrees. And the direction of that velocity is going to be be 30 degrees, 30 degrees upwards from the horizontal.

To launch a projectile, maybe it's a rock of some kind, with the velocity of So if the initial velocity is +5, then the final velocity has to be -5. However, we should easily see that the projectile was at first going up, but then it finishes by going down, thus we have to write the y component of the final velocity with the opposite sign of the y component of the initial velocity. And since the starting and ending points have the same elevation, we can then assume that the projectile has equal speed at those two points. We assume this to be true since we are also assuming that there is no air resistance. So we choose the final velocity to be just before it hits the ground.Īnd what is the final velocity before it hits the ground? Well, the projectile does not lose any energy while from the time right after it is launched to the time just before it lands. Fortunately, this problem can be solved just with the motion of the projectile before it hits the ground, so we don't need to concern ourselves with anything after that. Then only after it hits the ground will it have zero velocity, but hitting the ground will introduce another force to this system, and we would need to use more equations to describe its motion. Just before it hits the ground, the projectile has some downward speed. So we should only apply them to the motion of the projectile right after it is thrown and right before it hits the ground. This means that the only force acting on it is the force of gravity.
Projectile equation free#
The equations that we are using to solve this problem only apply when the projectile is in free fall.


 0 kommentar(er)
0 kommentar(er)
